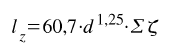Obliczenia hydrauliczne
Obliczenia hydrauliczne sieci cieplnych sprowadzają się najczęściej do wyznaczenia dwóch wielkości:
– średnicy wewnętrznej rurociągu
– straty ciśnienia w rurociągach na drodze przesyłu ciepła
Strata ciśnienia Δp jest sumą dwóch wielkości: straty liniowej ciśnienia Δpl spowodowanej tarciem nośnika ciepła o ścianki rur i start ciśnienia miejscowych „Z”, wywołanych oporami miejscowymi. Można to wyrazić wzorem:
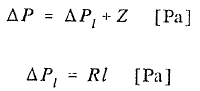(1)
gdzie:
R – współczynnik oporów liniowych [Pa/m]
l – długość rurociągu w [m]
Opory liniowe
Wyznaczenie strat liniowych można wykonać na podstawie wzoru Darcy’ego-Weisbacha
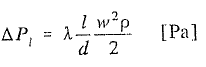(2)
gdzie:
λ – współczynnik oporu liniowego
l – długość rurociągu przesyłowego zasilającego i powrotnego [m]
w – prędkość przepływu czynnika w [m/s]
d- średnica wewnętrzna przewodu w [m]
ρ – gęstość nośnika ciepła w [kg/m3]
Wyznaczanie współczynnika λ
Współczynnik oporów liniowych zależy od wielu czynników. Dla przepływów laminarnych ( w sieciach takie praktycznie nie występują) współczynnik można wyznaczyć ze wzoru:
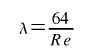
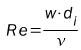gdzie Re liczba Reynoldsa, υ – współczynnik lepkości wody w danej temp.
Powyższy wzór jest słuszny dla wartości liczby Re <2300. W przypadku gdy Re>2300 rozpatrujemy dwa
obszary. Pierwszy, przejściowy gdy
2300 < Re ≤ 4000
czyli tzw. strefa krytyczna oraz drugi, gdy przepływ jest już ustabilizowany a Re > 4000. Dla obu tych obszarów wartość współczynnika oporów liniowych, z wystarczającą dokładnością, można wyznaczyć z zależności Waldena.
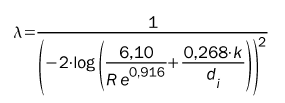
gdzie k – to chropowatość przewodów (dla rurociągów pracujących k=0,0005 m).
W przypadku dogłębniejszej analizy, należy, dla Re > 4000 sprawdzić czy ε spełnia zależność.
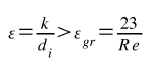
jeżeli nie, to współczynnik oporów liniowych wyznaczamy z wzoru Prandla-Karmana
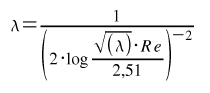
a jeśli ε > εgr to λ z wzoru Colebrooka-Whitea
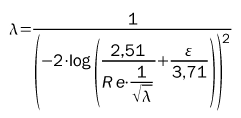
We wzorze (2) wielkością nieznaną jest prędkość przepływu czynnika grzejnego. Można ją wyznaczyć ze wzoru:
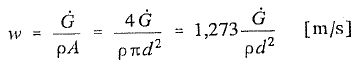(3)
gdzie:
G – strumień masy czynnika cieplnego w [kg/s]
A – pole przekroju wewnętrznego przewodu [m2]
Obliczając prędkość przepływu czynnika cieplnego należy przyjmować maksymalne prędkości przepływu:
2,0-3,0 m/s dla przewodów magistralnych
1,0-2,0 m/s dla odgałęzień od przewodu głównego
1,0 /s dla przyłączy do budynku
Podstawiając do wzoru na stratę liniową ciśnienia wartość prędkości „w” jw. otrzymamy:
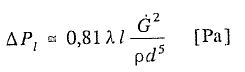(4)
Inne użyteczne wzory otrzymane na podstawie przekształceń:
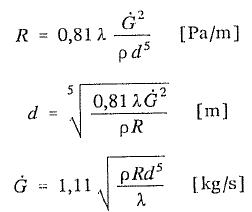(5)
Opory miejscowe
Spadek ciśnienia spowodowany oporami miejscowymi rurociągu Z można wyznaczyć ze wzoru:
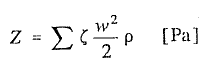(6)
gdzie:
ζ – współczynnik oporów miejscowych
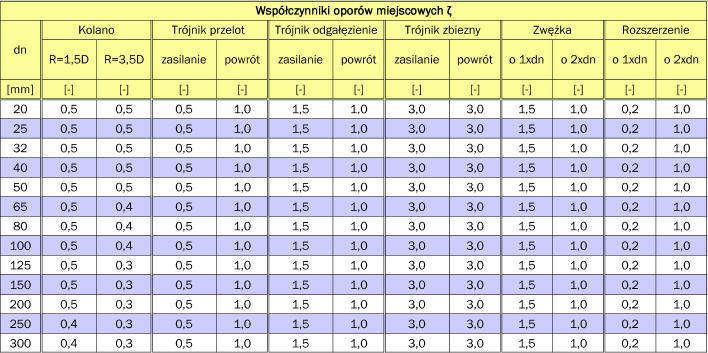
Tabela 1. Współczynniki oporów miejscowych.
Jeśli w powyższym wzorze za wartość prędkości podstawimy wzór (3), otrzymamy:
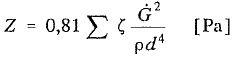(7)
W obliczeniach hydraulicznych często zamiast liczenia oporów miejscowych posługujemy się pojęciem długości zastępczej lz, która jest równa spadkowi ciśnienia równemu oporu liniowemu na przewodzie o tej samej średnicy. Długość zastępczą można wyznaczyć ze wzoru:
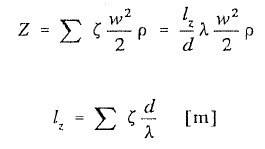(8)
Tabela 2 Długości zastępcze oporów miejscowych
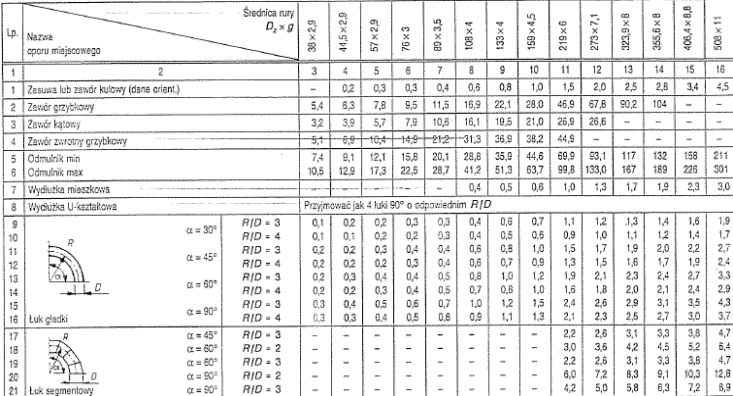
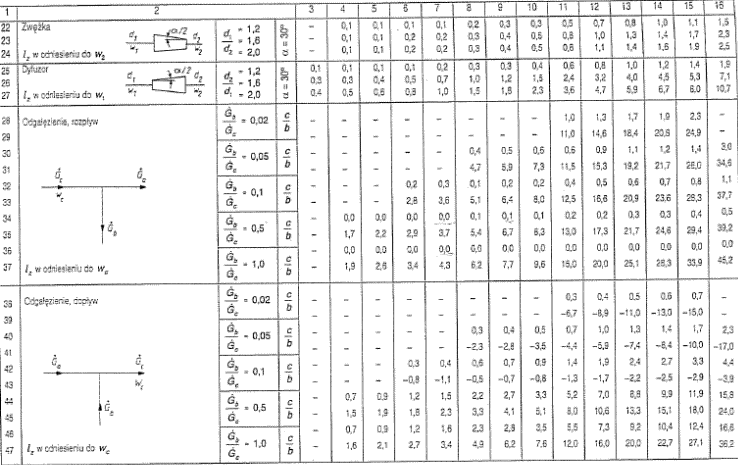
Dobór średnic przewodów
Praktyczny dobór średnic przewodów w sieci cieplnej sprowadza się do znalezienia wielkości strumienia ciepła na danej działce obliczeniowej i dobrania odpowiedniej średnicy z nomogramu lub tabeli. Obliczenia strumienia masy dla połączeń równoległych można wykonać ze wzoru:
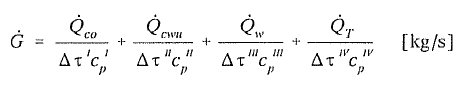(9)
gdzie:
Qco, Qcwu, Qw, QT – moc cieplna obliczana według wzorów omówionych w części trzeciej
Δτ’ – różnica temperatury obliczeniowej temperatury zasilania i powrotu w sezonie grzewczym [K]
Δτ” – różnica temperatury zasilania i powrotu poza sezonem grzewczym [K]
Δτ”’ – różnica temperatury zasilania i powrotu wody sieciowej przeznaczonej na potrzeby wentylacji [K]
ΔτIV – różnica temperatury zasilania i powrotu wody sieciowej przeznaczonej na potrzeby technologiczne [K]
Cp – ciepło właściwe wody dla odpowiadających wartości Δτ
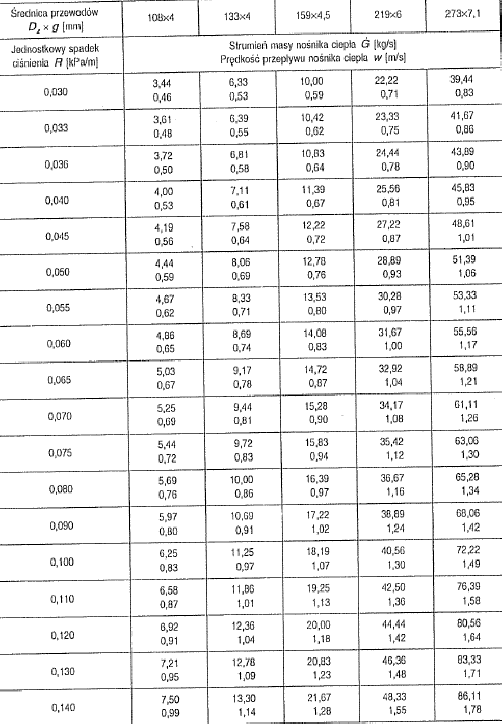
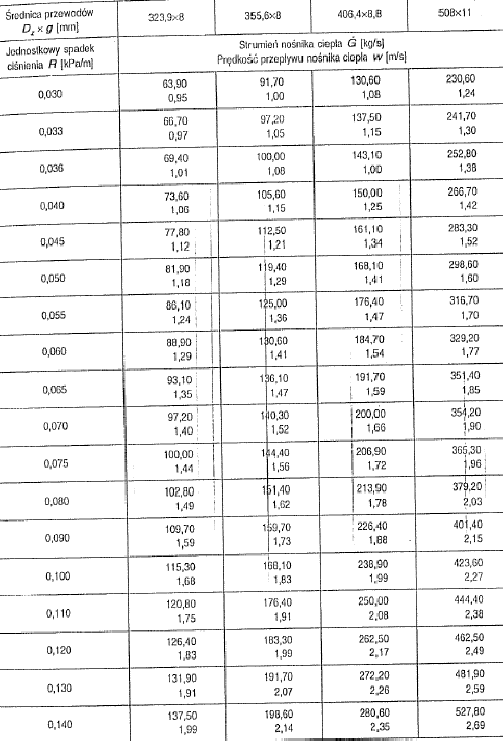
Poniżej w tablicy 1 podano wartości oporów miejscowych R i prędkości przepływu w dla danych wartości strumienia cieplnego G. W górnej części tabeli znajdują się wartości średnic przewodów sieciowych.
Tabela 3 Dobór średnic przewodów
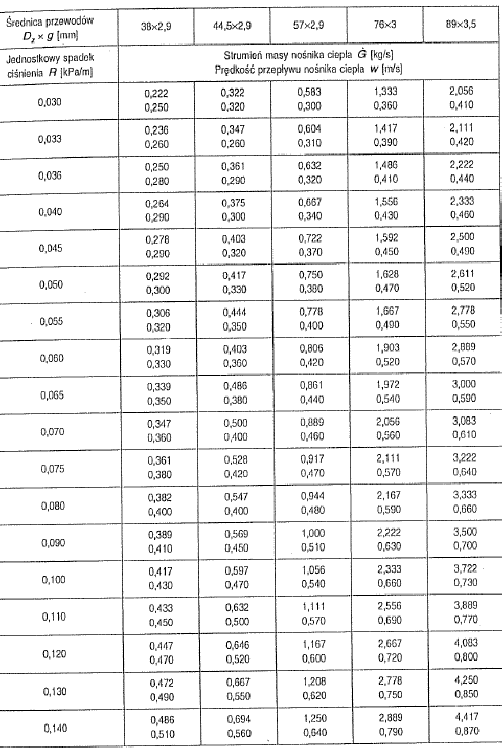
4.1 Obliczenia – wersja uproszczona
Przy dobieraniu średnic rur, określaniu liniowych strat ciśnienia czy przepustowości rurociągów można posłużyć się także wzorami uproszczonymi. W zakresie omawianych w katalogu średnic i stosowanym zakresie parametrów pracy sieci cieplnych niskich i wysokich parametrów, 10 % dokładność tych wzorów jest wystarczająca do wstępnego doboru i oszacowania poszukiwanych wartości. W pewnym zakresie wzory te z powodzeniem mogą nam zastąpić skomplikowane metody obliczeń dokładnych. Średnicę wewnętrzną rury przewodowej wodnej sieci cieplnej określić można z zależności:
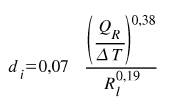
gdzie:
di – średnica wewnętrzna rury przewodowej wyrażona w [m],
QR – projektowana przepustowość rurociągu wyrażona w [kW],
ΔT – różnica temperatur czynnika na zasileniu i powrocie wyrażona w stopniach,
Rl – jednostkowy liniowy spadek ciśnienia w przewodzie (jako orientacyjny lub ekonomiczny spadek ciśnienia) wyrażony w [Pa/m].
Jednostkowy liniowy spadek ciśnienia w rurociągu wodnej sieci cieplnej o znanej średnicy wyznaczymy z wzoru:
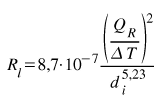
przy czym wzór ten sprawdza się dla średnic od dn=100 mm do dn=500 mm i obliczonych spadków w zakresie od 20 do 80 Pa/m, dając rozbieżności około +5 % dla dużych średnic. Dla średnic poniżej od dn=32 do dn=80 mm
można zastosować wzór postaci:
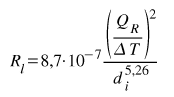
Oba wzory dla średnic dn=20 i dn=25 dają znaczne rozbieżności zaniżając wyniki.
Przepustowość wodnej sieci cielnej możemy z kolei wyznaczyć ze wzoru:
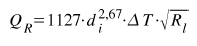
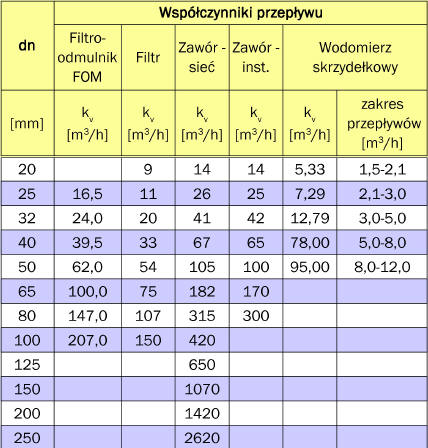
gdzie oznaczenia i jednostki jak poprzednio a dokładność wyników, w omówionym uprzednio zakresie spadków liniowych, wynosi około 7 % . Dla potrzeb obliczeń przybliżonych, w tabeli 4 zestawiono wartości współczynników
przepływu podstawowych urządzeń powszechnie stosowanych przez projektantów natomiast w tabeli 1 powyżej przedstawiono najczęściej stosowane wartości współczynników oporów miejscowych występujących w sieciach cieplnych.
Tabela 4 Wartości współczynników przepływu dla armatury sieci cieplnych.
Miejscowe straty ciśnienia, liczone na podstawie współczynników oporów miejscowych, wynoszą:
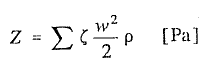
natomiast liczone na podstawie współczynników przepływu:
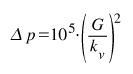
gdzie:
Z – opory miejscowe [Pa]
Σζ – suma współczynników oporów miejscowych [-],
kv – współczynnik przepływu [m3/h],
Δp – strata ciśnienia na urządzeniu [Pa],
G – przepływ objętościowy [m3/h],
ρ – ciężar właściwy wody [kg/m3],
g – przyspieszenie ziemskie [9,81 m/s2]
Ponadto, straty miejscowe wyrażone współczynnikiem oporów miejscowych można z powodzeniem przekształcić do tzw „zastępczej długości oporów miejscowych – lz” przy zastosowaniu wzoru:
